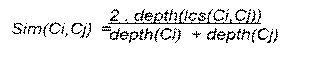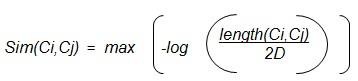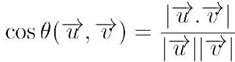novembro 19th, 2014
8077 views
Analysis of the use of different similarity functions in applications that use graph databases
|
|
Mauro André Barros Mazzola e Luciano Bernardes de Paula
Instituto Federal de Educação, Ciência e Tecnologia de São Paulo – IFSP
Área de Informática – Tecnólogo em Análise e Desenvolvimento de Sistemas
{Mazzola}mauroandre.mazzola@hotmail.com, {Paula}lbernardes@ifsp.edu.br
Resumo. Dada a quantidade dos dados disponíveis na Web, a maneira com que são organizados e o aumento dos mesmos, cada vez mais se torna necessário organizá-los para facilitar a realização de pesquisas por informações de forma coerente, levando em consideração o tipo de informação que se deseja obter. Os conceitos e padrões da Web Semântica dão suporte na organização e classificação dos diversos dados, o que permite uma busca conceitual, na qual o objetivo é recuperar não um dado específico, mas um grupo de dados que possuam certa similaridade conceitual. Este trabalho apresenta como utilizar funções de similaridade, que geram métricas de comparação entre objetos classificados em ontologias e bancos de dados baseados em grafo no auxílio à realização de buscas conceituais.
Palavras-chave: Web Semântica, banco de dados baseado em grafo, funções de similaridade, ontologias.
Abstract. As the amount of data available in the Web grows, so every day it is more important to organize these data aiming to make the retrieval of relevant data easier for the user. The concepts and standards of Semantic Web may be used as support to the organization and classification of several data, which allows the conceptual search, in which the goal is to retrieve a set of data that shares a common conceptual similarity. In this paper, it is presented how to use similarity functions, which generate metrics to be used to compare data, classified using an ontology, and graph databases to support the conceptual search.
Key words: Semantic Web, graph database, similarity function, ontology.
1. Introdução
A busca por um determinado dado na Web consiste, muitas vezes, no uso de palavras-chave que possivelmente devem existir no documento. Levando em conta o grande crescimento de informações que estão disponíveis todos os dias nos mais variados formatos, uma busca sobre determinado tema pode apresentar resultados nem sempre satisfatórios.
Como exemplo, pode ser citado a situação em que um usuário queira recuperar dados similares, independente do tipo (vídeos, textos, imagens, etc.), sobre um determinado assunto. Na busca tradicional, é possível a comparação de, por exemplo, um texto com outro texto, uma imagem com outra imagem e etc. Isso se dá pelo fato desses dados serem comparados de acordo com suas características (palavras-chave, tons de cores, etc). Porém, caso a busca seja realizada levando-se em consideração a classificação conceitual dos dados, diferentes tipos podem ser comparados, uma vez que essa comparação não considera suas características, mas sim sua classificação em um domínio de conhecimento.
Nesse contexto a Web Semântica contribui ao estabelecer maneiras de se adicionar significado aos dados, possibilitando a classificação conceitual (Berners-Lee, 2001). Para que a Web Semântica venha a ser colocada em prática, alguns padrões e ferramentas foram criados. A representação de um domínio é definida por meio de ontologias, nas quais os conceitos que compõem um determinado domínio têm seus significados e suas relações estabelecidas sendo, geralmente, representadas em grafos.
O RDF (Resource Description Framework) (W3C, 2014) descreve qualquer objeto que represente alguma informação, classificando-o em um domínio de conhecimento e apresentando suas relações com outros objetos que pertençam ao domínio, baseado em uma ontologia. A sintaxe do RDF se baseia no XML (Extensible Markup Language) (W3C, 2013) (Paula, 2011).
O OWL (Web Ontology Language) (W3C, 2012) descreve um domínio de conhecimento descrito em uma ontologia, considerando todos os conceitos e relações apresentados (Paula, 2011). OWL também é baseado em XML.
As funções de similaridade podem ser utilizadas para medir quanto algum objeto ou dado é similar a outro, a partir de medidas que definem o grau de similaridade entre eles. Essas funções retornam um valor entre 0 e 1, sendo que se a resposta obtida for mais próxima de 1, mais similares os dados são e quanto mais próximo a 0, menos similares são. Existem funções que medem a similaridade dos mais diversos tipos de dados como imagens, sons, textos, palavras, etc. Um dos tipos de funções de similaridade existentes compara a similaridade de um elemento a outro em uma estrutura como um grafo (Stasiu, 2007). Funções desse tipo podem ser utilizadas para a comparação semântica entre dois conceitos em uma ontologia representada como um grafo, como pode ser visto em (Paula, 2011).
Os bancos de dados baseados em grafos utilizam-se do conceito de grafos para indexar dados. Os dados são representados como vértices ou nós, sendo que cada nó também tem suas propriedades definidas conforme a necessidade. As arestas ligam um nó ao outro formando as relações, elas possuem um significado dentro do banco, podendo ter relações de diferentes tipos (Almeida, 2011). Bancos baseados em grafos se apresentam como uma opção natural a dados classificados por ontologias, uma vez que essas podem ser representadas por meio de grafos.
Este trabalho tem como objetivo apresentar como é possível usar funções de similaridade em busca de dados de maneira conceitual e como o uso de banco baseados em grafos pode ajudar na indexação dos dados.
O artigo está organizado da seguinte forma: a Seção 2 apresenta os conceitos da Web Semântica, a Seção 3 apresenta os conceitos de banco de dados baseado em grafo, a Seção 4 apresenta os conceitos de funções de similaridade, abordando os métodos utilizados nesta pesquisa, a Seção 5 apresenta os resultados obtidos, a Seção 6 apresenta a conclusão deste artigo.
2. Web Semântica
A Web Semântica pauta-se em organizar de modo conceitual os mais diversos dados disponíveis na Web, fazendo com que as máquinas passem a entender seu significado e assim obtenham melhores resultados na sua extração (Daniel Ferreira, 2008), (Paula, 2011), (Cordi, Lombardi, Martelli e Mascardi, 2005). Atualmente, a maior parte de dados disponíveis permite apenas interação humana e não com máquinas, visto que as mesmas não podem interpretá-las ou processá-las. Isso acontece devido à organização atual destes dados, na qual a maioria das consultas por algum tema é realizada através de palavras-chave, tipo de busca na qual os resultados obtidos podem nem sempre ser satisfatórios, exigindo assim uma interpretação humana para que estes dados sejam filtrados.
Segundo Berners-Lee, criador da WWW (World Wide Web), “A Web Semântica não é uma Web separada, mas uma extensão da atual. Nela a informação é dada com um significado bem definido, permitindo melhor interação entre computadores e as pessoas” (Berners-Lee, 2001). Com isso permite-se que não só pessoas passem a entender informações encontradas na Web, mas que máquinas, além de compreendê- las, possam também compartilhar estes conhecimento conforme a necessidade.
Compreendendo o grande desafio e dificuldade que é dar significado aos mais diversos dados de forma automática, ferramentas e padrões foram desenvolvidos, para dar suporte e fazer com que o ambiente da Web seja melhor aproveitado. Conceitos como ontologias, metadados, hierarquia de conceitos entre outros e tecnologias tais quais OWL, RDF, bancos de dados baseado em grafo e etc., vem a contribuir com esse contexto. A Figura 1 mostra a estrutura de camadas da Web Semântica, vale lembrar que a mesma não possui um modelo único de camadas, já que é uma tecnologia que está em processo de evolução (Paula, 2011).
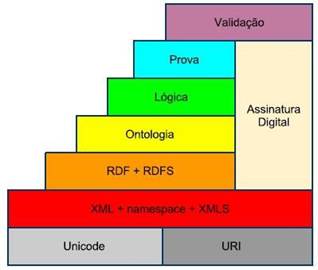
Figura 1. Camadas da Web Semântica
Baseado em (Paula, 2011), uma breve explicação das camadas presentes na Figura 1.
-
A camada URI (Uniform Resource Identifier) e Unicode definem o modo como os dados serão codificados, em relação à identificação e representação dos caracteres. O Unicode define um padrão para esses caracteres enquanto a URI é responsável por indicar onde o dado estará localizado.
-
Camada XML/XMLS (Extensible Markup Language Schema) e namespace determinam que os dados devam ser estruturados através de XML/XMLS e devem ter um namespace bem definido.
-
Utiliza-se a camada RDF/RDFS (Resource Description Framework Schema), para definir um modelo básico a ser apresentado de fato, sendo esse o RDF. Já o RDFS, em representação de uma estrutura conceitual simples, suas sintaxes de codificação se assemelham com a do XML.
-
A Ontologia, camada responsável por, organizar e classificar hierarquicamente dados de forma conceitual e organizada, compreendida como sendo a linguagem OWL, muito utilizada para esse fim no contexto da web semântica. A Figura 2 mostra uma ontologia criada no IFSP – Campus de Bragança Paulista, para um projeto de uma Rede Social Acadêmica.
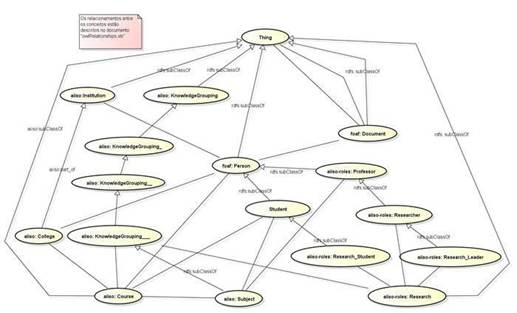
Figura 2. Ontologia, Rede Social Acadêmica
-
Camada lógica, responsável por melhorar e dar mais significado à camada de ontologia, vindo permitir determinação de conhecimentos declarativos específicos para algumas aplicações.
-
A camada de prova existe para realizar o processo de dedução e comprovação das informações que foram obtidas através das camadas abaixo dela.
-
Camada de validação, valida às assinaturas digitais de informações que foram processadas pelas camadas que se encontra abaixo dela. Sua grande importância se deve ao fato de ser essencial que os usuários confiem nos serviços que são oferecidos na semântica, dessa maneira pode se usufruir de toda sua funcionalidade.
A próxima seção apresenta conceitos dos bancos baseados em grafos, e sua utilização neste trabalho.
3. Banco de Dados Baseado em Grafo
Com a evolução natural que acontece na Ciência da Computação, várias ferramentas e conceitos passam a serem redefinidos, melhorados e criados, para dar suporte as mais diversas áreas que se apliquem as tecnologias computacionais (Stasiu, 2007). Levando em consideração esse cenário, um novo seguimento para bancos de dados são os baseados em grafos (Robinson, Webber e Eifrem, 2013).
A teoria dos grafos, criada por Euler no século XVIII, sempre foi motivo de estudo e melhorias por profissionais de várias áreas, tais como matemáticos, sociólogos, entre outros. Somente nos últimos anos é que essa teoria veio ser explorada para aplicar- se na gestão da informação (Robinson, Webber e Eifrem, 2013).
Os bancos de dados baseados em grafos indexam dados utilizando vértices (nós) e arestas (relações) de um grafo. Cada nó pode ter propriedades para indexar informações necessárias a ele. Diferente do que acontece em um banco de dados relacional, cada relação é explicitamente nomeada podendo também armazenar dados em propriedades que venham possuir. Isso faz com que sejam extremamente importantes, já que é possível realizar consultas através de suas propriedades e do tipo de relacionamento que venha a existir entre os nós.
Em (Almeida, 2011), o autor explora o seguinte problema: “Imagine uma aplicação que deve manter as informações relativas a viagens e locais onde pessoas moraram. Com isso, deve ser possível saber quando uma pessoa viajou ou qual o período em que ela viveu em determinada cidade”. Para resolução deste problema, são criados nós de dois tipos, classificando assim cada informação que deve ser indexada. Relações são geradas entre os nós, nomeando cada tipo de relação conforme a necessidade do problema, chegando à modelagem da Figura 3.
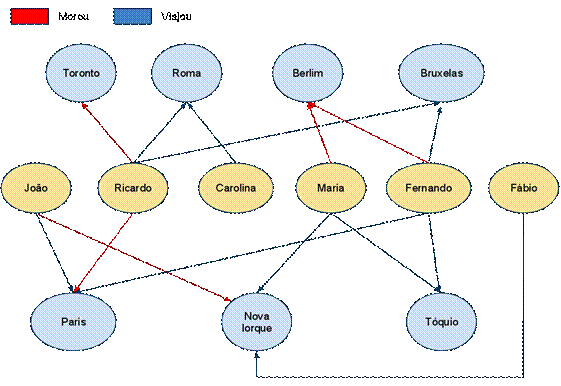
Figura 3. Modelagem Banco Baseado em Grafos (Almeida, 2011)
Em (Almeida, 2011) são mostradas a simplicidade e as facilidades que um banco baseado em grafo teria para trabalhar com consultas simples e outras mais complexas, comparando-o com modelo relacional, levando em consideração o contexto do domínio proposto. Como exemplo, baseado na Figura 3, considere uma pesquisa que retorne pessoas que viajaram para os mesmos lugares que Ricardo. O ponto de partida é o nó Ricardo e, recuperando os relacionamentos de saída do tipo Viajou, têm-se as cidades para onde ele viajou (Roma e Bruxelas). A partir das cidades, analisando os relacionamentos de entrada, também do tipo Viajou, chegam-se às pessoas Carolina e Fernando (Almeida, 2011). Como pode ser visto, uma navegação no grafo, levando-se em consideração o tipo de relação, possibilita que o resultado seja obtido.
Neste trabalho foi utilizado o banco baseado em grafo Neo4j (Neo4j, 2014), por ser uma ferramenta com uma versão gratuita, de fácil compreensão e com boa documentação (Finley, 2011).
A próxima seção apresenta as funções de similaridade e como essas são utilizadas no contexto de busca conceitual.
4. Funções de Similaridade
Uma vez que exista dados semanticamente classificados e organizados é interessante utilizar técnicas que venham permitir a realização de consultas, nas quais os resultados apresentados sejam mais relevantes e precisos conforme uma determinada necessidade.
Existem diversas funções de similaridade que calculam a semelhança dos mais variados tipos de dados, podendo obter o grau de similaridade entre imagens, textos, vídeos, conceitos em uma ontologia, entre outros (Stasiu, 2007). É interessante notar que, ao utilizar funções que calculem a similaridade entre dados classificados em conceitos dentro de uma ontologia, o resultado será abrangente em relação ao tipo de dado pesquisado, já que qualquer dado pode ser classificado em um modelo ontológico. A Figura 4 exemplifica esse contexto, no qual o conceito “F” representa Girafas e o conceito “D” Peixes.
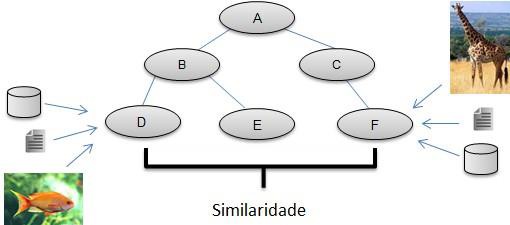
Figura 4. Classificação de Dados Conceitualmente
Esses conceitos são derivados dos conceitos “B” e “C”, que, por exemplo, poderiam ser os conceitos “Animais Aquáticos” e “Animais Terrestres”, respectivamente. Por sua vez, os conceitos “B” e “C” são derivados do conceito “A”, que poderia ser algo mais genérico, como “Animais”. Baseado nessa ontologia, qualquer dado independente do tipo (texto, vídeo, imagem, etc) pode ser classificado em uma mesma categoria ou conceito. Todos os conceitos que pertencem a uma ontologia possuem alguma similaridade entre si, sendo determinados conceitos mais, ou menos, similares a outros. Essa medida de similaridade entre os conceitos irá depender do domínio ontológico e da estratégia utilizada pela função de similaridade que venha a ser utilizada.
Essas funções utilizam múltiplas estratégias ao executar o cálculo, a partir da implementação de algoritmos específicos para cada tipo de dado a ser analisado, sendo que o grau de similaridade entre termos de um universo U pode ser definido da seguinte forma:
sim(a,b) = [0,1]
Sendo a e b objetos que pertencem a um determinado conjunto U, os mesmos são comparados por uma função de similaridade que resulta em um valor entre 0 e 1. Quanto mais próximo ao valor 1, os objetos são considerados mais similares, o contrário, quanto mais próximo a 0, menos similares eles são. Utilizando uma das funções de similaridade consegue-se realizar a comparação entre um objeto com todos outros n objetos contidos em domínio U, resultando assim em um ranking com a similaridade de todos os objetos que compõem este domínio entre si (Stasiu, 2007).
Os métodos para comparação de similaridade entre dados classificados em uma ontologia representada por grafo utilizado nesta pesquisa levam em conta aspectos da topologia de uma ontologia como, por exemplo, sua profundidade, o menor caminho entre dois conceitos e a profundidade do primeiro conceito em comum entre dois conceitos. Existem também outros métodos que verificam a similaridade, através do conteúdo da informação da ontologia, e um terceiro com base em um glossário (Cordi, Lombardi, Martelli e Mascardi, 2005), (Paula, 2011), mas que estão além do escopo deste trabalho. Todas as funções aqui apresentadas foram implementadas e a ontologia utilizada em todos os testes realizados é a representada na Figura 5. A seguir são mostradas algumas funções de similaridade.
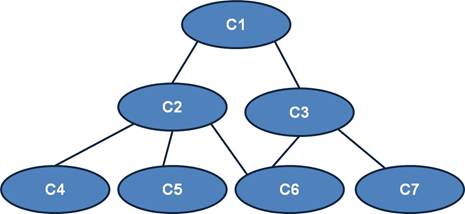
Figura 5. Modelo Ontológico
Método do Menor Caminho
Apresentado em (Bouquet, Kuper, Scoz, e Zanobini, 2004), os autores definem distâncias entre os conceitos, representadas por Ds(Ci, Cj), sendo que Ci e Cj o menor caminho entre os conceitos analisados. Caso não exista um menor caminho é atribuído o valor 0 (Paula, 2011). Na Tabela 1 é mostrado qual seriam as distâncias para ontologia da Figura 5, sem ser levada em conta a normalização do método menor caminho.
T1. Distâncias Entre Conceitos.
Conceito
|
C1
|
C2
|
C3
|
C4
|
C5
|
C6
|
C7
|
C1
|
0
|
1
|
1
|
2
|
2
|
2
|
2
|
C2
|
1
|
0
|
2
|
1
|
1
|
1
|
3
|
C3
|
1
|
2
|
0
|
3
|
3
|
1
|
1
|
C4
|
2
|
1
|
3
|
0
|
2
|
2
|
4
|
C5
|
2
|
1
|
3
|
2
|
0
|
2
|
4
|
C6
|
2
|
1
|
1
|
2
|
2
|
0
|
2
|
C7
|
2
|
3
|
1
|
4
|
4
|
2
|
0
|
Após saber as distâncias, podem-se normalizar todas, dividindo o valor de cada posição pelo maior caminho que existir. Para que a função retorne valores no intervalo de [0, 1], e conste maior similaridade entre os conceitos que estejam mais próximos, invertem-se os valores, sendo seu cálculo determinado por 1 – Ds (Ci, Cj) (Paula, 2011). Os resultados da obtidos através da função do menor caminho, conforme a ontologia utilizada é apresentado na Tabela 2.
Tabela 2. Similaridade Método Menor Caminho.
Conceito
|
C1
|
C2
|
C3
|
C4
|
C5
|
C6
|
C7
|
C1
|
1
|
0,75
|
0,75
|
0,5
|
0,5
|
0,5
|
0,5
|
C2
|
0,75
|
1
|
0,5
|
0,75
|
0,75
|
0,75
|
0,25
|
C3
|
0,75
|
0,5
|
1
|
0,25
|
0,25
|
0,75
|
0,75
|
C4
|
0,5
|
0,75
|
0,25
|
1
|
0,5
|
0,5
|
0
|
C5
|
0,5
|
0,75
|
0,25
|
0,5
|
1
|
0,5
|
0
|
C6
|
0,5
|
0,75
|
0,75
|
0,5
|
0,5
|
1
|
0,5
|
C7
|
0,5
|
0,25
|
0,75
|
0
|
0
|
0,5
|
1
|
Método Profundidade da Ontologia
Esse método é exibido em (Wu e Palmer, 1994), no qual os autores exploram e mostram as dificuldades que são encontradas na tradução automática entre línguas. É apresentada uma métrica que vem a ser redefinido em (Resnik, 1999), chegando a seguinte representação:
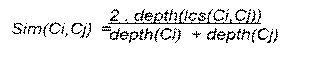
sendo depth(Cn) a distância de algum conceito Cn para raiz, lcs(Ci,Cj) seria o primeiro conceito em comum encontrado no caminho de Ci e Cj. Conforme o lcs de dois conceitos esteja em um nível mais profundo, e Ci, Cj venham situar-se próximos na ontologia, faz com que os conceitos sejam mais similares, e quanto mais diferente deste cenário menos similares serão. Por essa função, caso lcs venha a ser a raiz da ontologia não existirá similaridade entre dois termos, portanto não poderá existir semântica entre conceitos que se localizem em ramos diferentes da ontologia sendo o conceito raiz o primeiro em comum (Paula, 2011). Os resultados retornados desta função são mostrados na Tabela 3.
Tabela 3. Similaridade Método Profundidade da Ontologia.
Conceito
|
C1
|
C2
|
C3
|
C4
|
C5
|
C6
|
C7
|
C1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
C2
|
0
|
1
|
0
|
0,67
|
0,67
|
0,67
|
0
|
C3
|
0
|
0
|
1
|
0
|
0
|
0,67
|
0,67
|
C4
|
0
|
0,67
|
0
|
1
|
0,5
|
0,5
|
0
|
C5
|
0
|
0,67
|
0
|
0,5
|
1
|
0,5
|
0
|
C6
|
0
|
0,67
|
0,67
|
0,5
|
0,5
|
1
|
0,5
|
C7
|
0
|
0
|
0,67
|
0
|
0
|
0,5
|
1
|
Método Menor Caminho Escalado
Em (Leacock e Chodorow, 1998) os autores abordam o problema de se encontrar o significado de palavras em uma taxonomia. Para isso definem a seguinte equação:
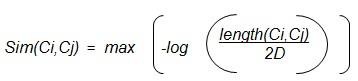
Sendo length(Ci,Cj) a distância entre Ci e Cj, D é a profundidade máxima da ontologia. O menor caminho entre os conceitos será gerado a partir do maior valor retornado por essa equação. Acaba sendo o método do menor caminho sobre a escala da profundidade, tendo uma distribuição logarítmica (Paula, 2011). Os resultados retornados por esse método são mostrados na Tabela 4.
Tabela 4. Similaridade Método Menor Caminho Escalado.
Conceito
|
C1
|
C2
|
C3
|
C4
|
C5
|
C6
|
C7
|
C1
|
1
|
0,6
|
0,6
|
0,3
|
0,3
|
0,3
|
0,3
|
C2
|
0,6
|
1
|
0,3
|
0,6
|
0,6
|
0,6
|
0,12
|
C3
|
0,6
|
0,3
|
1
|
0,12
|
0,12
|
0,6
|
0,6
|
C4
|
0,3
|
0,6
|
0,12
|
1
|
0,3
|
0,3
|
0
|
C5
|
0,3
|
0,6
|
0,12
|
0,3
|
1
|
0,3
|
0
|
C6
|
0,3
|
0,6
|
0,6
|
0,3
|
0,3
|
1
|
0,3
|
C7
|
0,3
|
0,12
|
0,6
|
0
|
0
|
0,3
|
1
|
Método que Combina Menor Caminho e Profundidade
Os autores em (Li, Bandar, e Mclean, 2003) apresentam que para chegar à semântica entre duas palavras deve-se considerar a distância entre elas, a profundidade, e a densidade local, chegando à equação:

Sendo l a menor distância que existe entre Ci e Cj, h será a profundidade do primeiro conceito direto em comum. É indicado em (Li, Bandar, e Mclean, 2003) que o melhor valor para αé 0,2, e para βseria 0,6.
Quando Ci e Cj são diferentes, no começo da equação 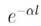 , a similaridade é maior, logo que o valor de l seja baixo, no restante conforme o valor de h seja maior o grau de similaridade é aumentado (Paula, 2011). As similaridades obtidas utilizando esse método conforme a ontologia utilizada é mostrada na Tabela 5.
, a similaridade é maior, logo que o valor de l seja baixo, no restante conforme o valor de h seja maior o grau de similaridade é aumentado (Paula, 2011). As similaridades obtidas utilizando esse método conforme a ontologia utilizada é mostrada na Tabela 5.
Tabela 5. Similaridade Método Combinação Entre Menor Caminho e Profundidade.
Conceito
|
C1
|
C2
|
C3
|
C4
|
C5
|
C6
|
C7
|
C1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
C2
|
0
|
1
|
0
|
0,44
|
0,44
|
0,44
|
0
|
C3
|
0
|
0
|
1
|
0
|
0
|
0,44
|
0,44
|
C4
|
0
|
0,44
|
0
|
1
|
0,36
|
0,36
|
0
|
C5
|
0
|
0,44
|
0
|
0,36
|
1
|
0,36
|
0
|
C6
|
0
|
0,44
|
0,44
|
0,36
|
0,36
|
1
|
0,36
|
C7
|
0
|
0
|
0,44
|
0
|
0
|
0,36
|
1
|
Similaridade pela Representação dos Conceitos em um Espaço Vetorial
A técnica “Modelo avançado de espaço vetorial baseado em tópicos” (Enhanced Topic- based Vector SpaceModel (eTVSM)), mostra uma representação dos conceitos que pertencem a uma determinada ontologia em um espaço vetorial (Polyvyanyy, 2007).
No eTVSM, é criado um vetor para cada conceito da ontologia, calculando a similaridade através do cosseno do ângulo entre dois vetores. Para obter os valores em cada par de vetores, é utilizado o seguinte algoritmo: primeiro geram-se os vetores para conceitos folhas, ou seja, conceitos que não possuem nenhum descendente. O vetor irá receber o valor 1 para cada ascendente do conceito a ser analisado que esteja no caminho entre o conceito e a raiz e pra ele mesmo. Para os demais conceitos seu valor será 0. Levando em consideração a ontologia de testes utilizada, os conceitos folhas seriam C4, C5, C6 e C7, sendo os vetores criados referente à C6 e C7, respectivamente, vetC6 = {1, 1, 1, 0, 0, 1, 0} e vetC7 = {1, 0, 1, 0, 0, 0, 1}. Os conceitos não folhas tem seu vetores criados a partir da soma vetorial dos seus descendentes diretos, sendo assim o vetor de C2 seria gerado pela soma dos vetores de C4, C5 e C6 (Polyvyanyy, 2007) (Neves, 2010/2011).
Os valores de todos os vetores já normalizados seriam (Paula, 2011):
C1 = {0,669, 0,495, 0,429, 0,120, 0,120, 0,255, 0,174}
C2 = {0,642, 0,642, 0,194, 0,224, 0,224, 0,194, 0}
C3 = {0,607, 0,282, 0,607, 0, 0, 0,282, 0,325}
C4 = {0,577, 0,577, 0, 0,577, 0, 0, 0}
C5 = {0,577, 0,577, 0, 0, 0,577, 0, 0}
C6 = {0,5, 0,5, 0,5, 0, 0, 0,5, 0}
C7= {0,577, 0, 0,577, 0, 0, 0, 0,577}
Para obter os cossenos entre os ângulos dos vetores utilizamos o seguinte cálculo:
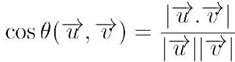
Sendo 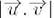 o produto escalar entre eles,
o produto escalar entre eles, 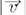 o tamanho do vetor, como visto em (Paula, 2011). A Tabela 6 apresenta valores calculados conforme o método eTVSM.
o tamanho do vetor, como visto em (Paula, 2011). A Tabela 6 apresenta valores calculados conforme o método eTVSM.
Tabela 6: Método eTVSM.
Conceito
|
C1
|
C2
|
C3
|
C4
|
C5
|
C6
|
C7
|
C1
|
1
|
0,933
|
0,933
|
0,741
|
0,741
|
0,924
|
0,734
|
C2
|
0,933
|
1
|
0,742
|
0,871
|
0,871
|
0,836
|
0,438
|
C3
|
0,933
|
0,742
|
1
|
0,513
|
0,513
|
0,888
|
0,888
|
C4
|
0,741
|
0,871
|
0,513
|
1
|
0,667
|
0,577
|
0,333
|
C5
|
0,741
|
0,871
|
0,513
|
0,667
|
1
|
0,577
|
0,333
|
C6
|
0,924
|
0,836
|
0,888
|
0,577
|
0,577
|
1
|
0,577
|
C7
|
0,734
|
0,483
|
0,888
|
0,333
|
0,333
|
0,577
|
1
|
Comparação Entre os Métodos
Existem diversos tipos de funções que geram valores de similaridade para uma ontologia de conceitos. Como foi mostrado há diferentes parâmetros que ajudam a realizar o cálculo da semântica entre conceitos, como, o menor caminho entre eles, a altura de determinado conceito em relação à raiz, a profundidade da ontologia, a altura de um conceito em comum, entre outros, sendo cada um desses aspectos utilizados de acordo com objetivo de cada função.
É interessante perceber que em determinados domínios, uma função de similaridade pode trazer melhores resultados que outras, ou seja, não existe uma função que venha a ser melhor em relação às demais, visto que cada uma delas aborda estratégias diferentes que devem ser levadas em consideração juntamente com o domínio que se esta trabalhando no momento de escolha de uma função.
Por exemplo, em uma ontologia na qual o conceito raiz é mais genérico, seus descendentes mesmo que diretos podem representar áreas de conhecimento extremamente distintas, diferentemente de uma ontologia na qual a raiz possa ser um conceito mais específico, na qual seus descendentes diretos possuam certa relevância. Para cada ontologia, uma determinada função retorna valores mais satisfatórios em relação a outras.
Não seria recomendável utilizar a função do menor caminho, ou do menor caminho escalado para uma ontologia com a raiz definida por um conceito genérico, pois esses métodos retornam valores mais elevados para os conceitos que se encontram próximos, independente da altura que estes estejam. No entanto com uma ontologia com a raiz representada por um conceito mais específico (como no exemplo da Figura
4), não seria interessante utilizar os métodos da profundidade e combinação entre menor caminho e profundidade, devido a esses métodos definirem que não existe nenhum um grau de semântica em conceitos onde o primeiro em comum seja a raiz. Reforçando é necessário entender os métodos e suas estratégias, para obter bons resultados na busca de similaridade entre conceitos.
5. Resultados
A metodologia utilizada nesse trabalho é de uma pesquisa aplicada, com abordagem qualitativa, objetivos descritivos e exploratórios. Os procedimentos técnicos envolvidos foram a pesquisa bibliografia e o estudo de caso.
Para realizar testes foram criados dois ambientes, utilizando o Neo4J, com base na ontologia utilizada, para a qual foram gerados os valores de similaridade. O primeiro leva em consideração valores gerados a partir do método da profundidade, o segundo utiliza resultados obtidos pela função eTVSM. Indexando os valores retornados, nas propriedades dos nós conceituais, será apresentada duas queries para cada ambiente, e uma query de comparação. Ambas as funções escolhidas levam em consideração o domínio criado neste artigo.
Primeiro Ambiente
Esse ambiente foi elaborado levando em consideração a ontologia apresentada na Figura 6. A raiz é genérica, definida pelo conceito Coisa. Este domínio define Pessoas e Esportes. Dois tipos de relações foram criados, entre os nós que definem conceitos da ontologia a relação é do tipo similar, já nós conceituais e nós que são classificados por um determinado conceito a relação e do tipo “é um”. Foram indexados três nós com relação do tipo “é um” em cada um dos conceitos Ator, Musico, Jogador e Modalidade.
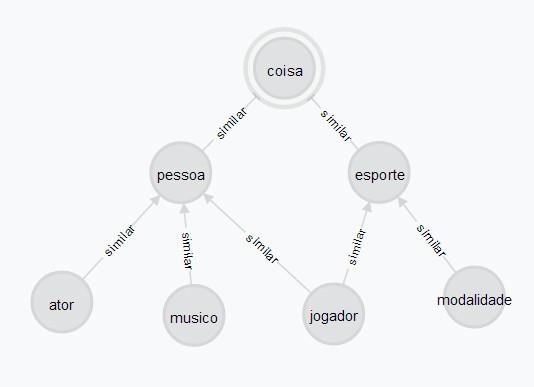
Figura 6. Ambiente 1.
Ao realizar uma consulta que retorne todos os conceitos que venham a ser similar até
0,6 com Esporte (Figura 7) são retornados os conceitos Esporte, Jogador e
Modalidade, conforme o esperado, levando em consideração o método da profundidade (Resnik, 1999). Vale lembrar que sim2 é a propriedade na qual estão indexados os valores de similaridade para o conceito Esporte em todos os nós conceituais, e type armazena o tipo do nó.
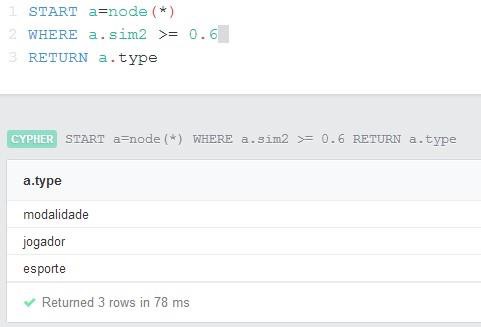
Figura 7. Query 1
Ao pesquisar resultados que sejam similares até 0,5 com o conceito Ator (Figura 8), levando em consideração as relações do tipo “é um”, o retorno será, nós relacionados com conceito Ator e outros tipos de Pessoa. Isso se deve, à subclassificação de Músico e Jogador com conceito Pessoa, no contexto da função de similaridade da profundidade.
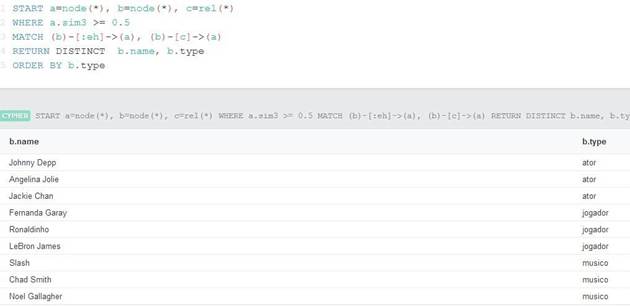
Figura 8. Query 2
Segundo Ambiente
Esse ambiente foi elaborado conforme a ontologia da Figura 9. A raiz não é genérica, definida pelo conceito Pessoa. Este domínio define pessoas em um ambiente acadêmico. Como no ambiente 1, para diferenciar as relações existentes no modelo, os mesmos dois tipos de relações foram criados, entre nós conceituais e nós que são classificados por um determinado conceito a relação e do tipo “é um”, e para os nós que definem conceitos da ontologia a relação é do tipo “similar”. Foram indexados três nós com relação do tipo “é um” em cada um dos conceitos, Professor e Aluno.
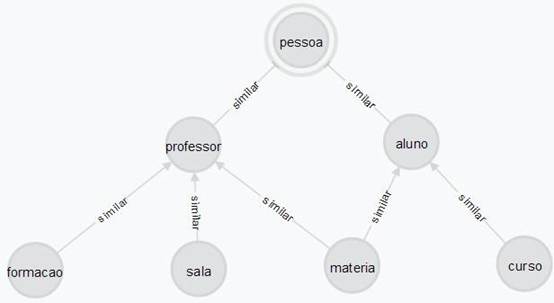
Figura 9. Ambiente 2
Ao consultar os conceitos que tenham similaridade até 0,7 com Curso (Figura 10), são retornados os conceitos Curso, Aluno e Pessoa, conforme o esperado para o método eTVSM.
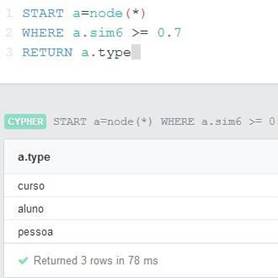
Figura 10. Query 3
Buscar por nós com ligações do tipo “é um”, similares até 0,7 com o conceito Professor (Figura 11), tem como resultado, nós relacionados aos conceitos Professor e Aluno, isso se deve a forma como método eTVSM considera a similaridade. A consulta da Figura 11 retorna os nomes dos nós, o tipo qual estão classificados conceitualmente (nós conceituais), e sua similaridade com o conceito Professor.
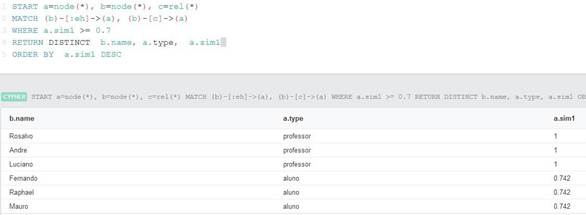
Figura 11. Query 4
Análise comparativa entre os diferentes métodos
A fim de comparar os resultados entre os métodos de similaridade, foi realizada a mesma consulta da Figura 4, recuperar nós com relações do tipo “é um”, similares até 0,7 com o conceito Professor (Figura 12). Utilizando o ambiente 2, mas indexando aos nós conceituais valores obtidos através do método da profundidade. Como resultado, retornam-se os nós que estão classificados pelo conceito Professor. Isso se deve a forma como a função da profundidade considera a similaridade, sendo que por estar em ramificações opostas na ontologia, o valor de similaridade entre os conceitos Professor e Aluno é zero.
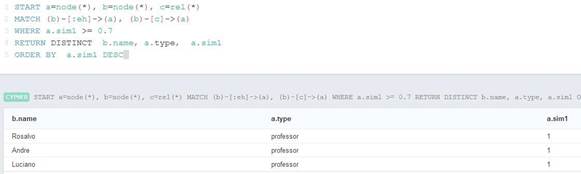
Figura 12.Query 5
Com isso é possível notar a importância da escolha por uma função de similaridade em relação ao domínio que se deve trabalhar, a escolha de uma função interfere diretamente na qualidade dos dados recuperados em uma consulta, considerando um determinado domínio. No ambiente 2 ao indexar valores semânticos referente a função da profundidade fizemos com que Professor e Aluno não possuíssem nenhum grau de similaridade, já que o primeiro conceito em comum entre eles é o conceito raiz definido como Pessoa, dependendo da maneira que se deseja trabalhar com esse novo ambiente, os resultados recuperados podem não ser satisfatórios para um usuário.
Percebe-se também que se for utilizada a função eTVSM para gerar valores de similaridade entre conceitos no ambiente 1, a consulta realizada na Figura 8 retornará os mesmos dados, porém ao verificarmos o valor de similaridade entre o conceito Ator e os conceitos Musico e Jogador os resultado são diferentes dos que foram recuperados utilizando o método da profundidade, no qual sim(Ator,Musico)=0,5 e sim(Ator,Jogador)=0,5. Utilizando eTVSM os valores são sim(Ator,Musico)= 0,667 e sim(Ator,Jogador)= 0,577. Percebe-se que nesse caso um ator é mais similar a um músico que a um jogador, sendo que dependendo de como se queira utilizar esse ambiente isso pode ser menos ou mais favorável a recuperar dados relevantes.
Os testes realizados buscaram recuperar dados classificados de forma conceitual, a partir do grau de similaridade entre eles. Tanto a busca por conceitos, quanto a de dados classificados nestes conceitos, retornaram resultados esperados, para cada ambiente criado, levando em conta os métodos que foram utilizados para os testes.
6. Conclusão
A indexação dos valores gerados a partir das funções de similaridade no banco visou obter o melhor resultado levando em consideração o domínio das ontologias, que vieram ser criadas para os testes. As consultas feitas apresentaram uma busca conceitual para dados indexados com determinada relação que pode vir a existir entre diferentes nós. Podemos perceber que a busca por similaridade é possível de ser realizada e pode retornar resultados precisos conforme o grau de similaridade que seja necessário.
Utilizando buscas conceituais, é possível responder a eventuais questões como, “Me retorne documentos que são similares até 0,7 com conceito X”. Sendo assim, o resultado da busca será mais preciso com a necessidade de um usuário. Foram mostrados alguns métodos de similaridade e discutiu-se o fato de cada um ser mais bem indicado para diferentes cenários de classificação de dados.
Em trabalhos futuros, podem-se buscar novos métodos para realizar o cálculo de similaridades entre conceitos de uma ontologia, estudando os domínios que venham a serem utilizados, além de aprofundar os estudos na indexação de ontologias em bancos de dados baseados em grafos, tais qual realização de consultas que venham a ser necessárias para um determinado sistema, assim como novas estratégias para indexar e realizar pesquisas com similaridade.
Referências
SILVA, DANIEL FERREIRA DA. Estudo de funções de similaridade semântica de termos aplicadas a um domínio. [Recife], PE. 2008. 45p.
PAULA, LUCIANO BERNARDES DE. Utilização de funções LSH para busca conceitual baseada em ontologias. UNIVERSIDADE ESTADUAL DE CAMPINAS FACULDADE DE ENGENHARIA ELÉTRICA E DE COMPUTAÇÃO DEPARTAMENTO DE COMPUTAÇÃO E AUTOMAÇÃO INDUSTRIAL, 2011, Campinas – SP.
STASIU, RAQUEL KOLITSKI. Avaliação da Qualidade de Funções de Similaridade no Contexto de Consultas por Abrangência. PhD thesis,
INSTITUTO DE INFORMÁTICA, UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL, 2007.
VALENTINA CORDI , PAOLO LOMBARDI , MAURIZIO MARTELLI; VIVIANA MASCARDI. An ontology-based similarity between sets of concepts. Genova, Itália. 2005. 16–21p.
BOUQUET, P.; KUPER, G.M.; SCOZ, M.; AND ZANOBINI, S. Asking and answering semantic queries. In WORKSHOP ON MEANING COORDINATION AND NEGOTIATION WORKSHOP (MCN-04) IN CONJUNCTION WITH THE 3RD INTERNATIONAL SEMANTIC WEB CONFERENCE (ISWC-04), Hiroshima, Japan, November 2004.
WU, ZHIBIAO; PALMER, MARTHA. Verb semantics and lexical selection. 1994. 133–138p.
RESNIK, PHILIP. Semantic similarity in a taxonomy: An information-based measure and its applicationto problems of ambiguity in natural language. Journal of Artificial Intelligence Research, 1999. 95–130p.
LEACOCK, C.; CHODOROW, M. Combining local context and wordnet similarity for word sense identification. In Fellbaum MIT Press. 1998.
LI, Y; BANDAR, Z.A.; MCLEAN, D. An approach for measuring semantic similarity between words using multiple information sources. Knowledge and Data Engineering, IEEE Transactionson. 2003. 15(4):871–882p.
NEVES, RICARDO FERNANDO MUACHO FERNANDES LIMA. Classificação Automática de Textos Baseada em Ontologias, UNIVERSIDADE NOVA DE LISBOA FACULDADE DE CIÊNCIAS E TECNOLOGIA DEPARTAMENTO DE INFORMÁTICA 2009/2010.
ROBINSON, IAN; WEBBER, JIM AND EIFREM, EMIL, Graph Databases. Early release revision 1, 2013. 189p.
W3C. Extensible Markup Language (XML). Disponível em <http://www.w3.org/XML/> Acesso em: 26 abr. de 2014. 2013.
W3C. Resource DescriptionF ramework (RDF). Disponível em <http://www.w3.org/RDF/> Acesso em: 26 abr. de 2014. 2014.
W3C. Web Ontology Language(OWL). Disponível em <http://www.w3.org/OWL/> Acesso em: 26 abr. de 2014. 2012.
POLYVYANYY, ARTEM. Evaluation of a novel information retrieval model: etvsm. Master’s thesis, HASSO PLATTNER INSTITUT, UNIVERISTAT POTSDM, 2007.





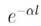 , a similaridade é maior, logo que o valor de l seja baixo, no restante conforme o valor de h seja maior o grau de similaridade é aumentado (Paula, 2011). As similaridades obtidas utilizando esse método conforme a ontologia utilizada é mostrada na Tabela 5.
, a similaridade é maior, logo que o valor de l seja baixo, no restante conforme o valor de h seja maior o grau de similaridade é aumentado (Paula, 2011). As similaridades obtidas utilizando esse método conforme a ontologia utilizada é mostrada na Tabela 5.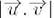 o produto escalar entre eles,
o produto escalar entre eles, 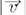 o tamanho do vetor, como visto em (Paula, 2011). A Tabela 6 apresenta valores calculados conforme o método eTVSM.
o tamanho do vetor, como visto em (Paula, 2011). A Tabela 6 apresenta valores calculados conforme o método eTVSM.